A recursion is problem-solving method which calls itself in a range of calls until the base one. Only the base call is defined with clear solution; other ones are derived from it. A base call finally terminates the recursive function. Recursive techniques can be short and simple, but sometimes hard to figure out the proper setup. There is number of problems that are traditionally solved by recursion. Note that for every solvable problem it is possible to use either recursion or iteration. Here we present famous puzzle called “Towers of Hanoi”, explain the input premises, define logarithm in pseudo code, and finally craft an implementation of the algorithm (we will use Python). We conclude by evaluating the code, dissecting it step by step.
Premises of Towers of Hanoi puzzle
Suppose we have three rods, or towers, with a number of disks on one rod. Disks are sorted according to their diameter, from largest one being on the bottom, to smallest one on the top. The goal is to move those disks in the same sorted manner onto another tower, respecting the following rules:
- The disks are moved in turns. It is allowed to move only one disk per turn.
- The move consists of moving the one disk from one tower to another one. Towers are marked as a source, destination and auxiliary ones. Their order is not fixed, i.e., all of three can bear any of those three names.
- It is allowed moving either disk on an empty tower, or, if the tower contains disk(s), only smaller disk may be placed onto bigger one.
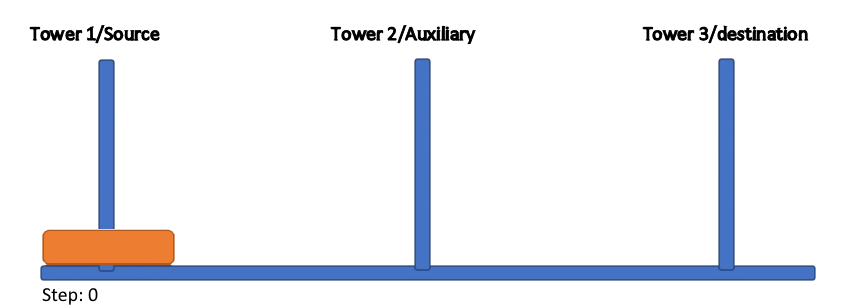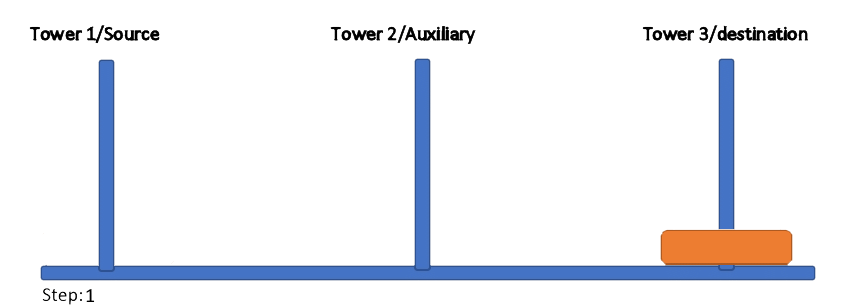
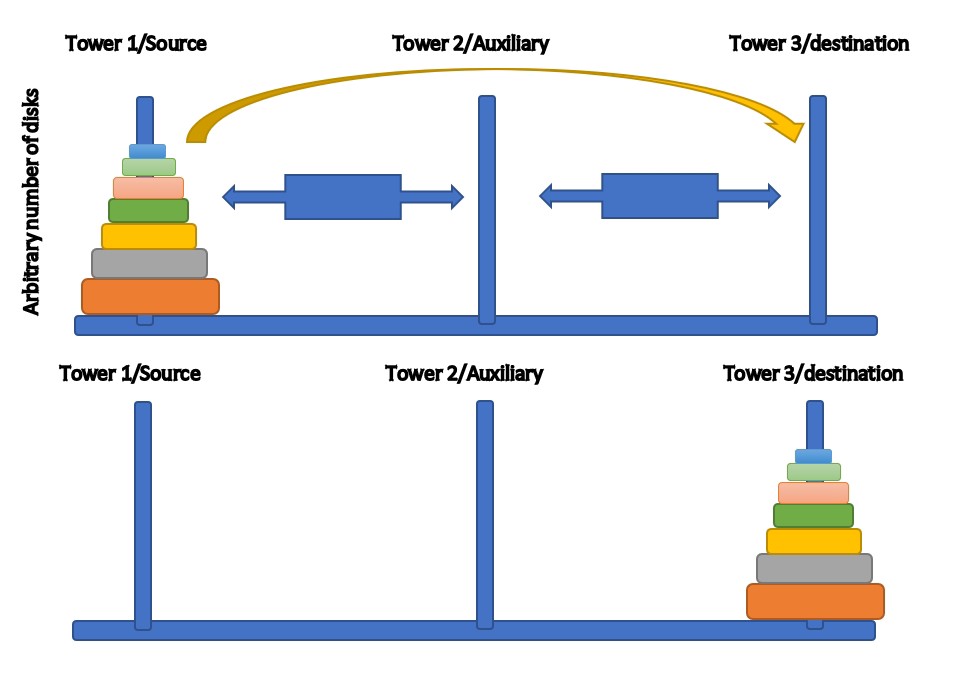Figure 1: Generalized depiction of the problem and solution
Discussing the possible solutions
Recursive problems can be divided to subproblems of similar type. In our problem setup, we label the number of disks as n. The simplest subproblem would be when we have only one disk, i.e., when n=1.
Figure 2: Solution where n=1
It is obvious that, in the case of n=1, problem is solvable in one step, by simply moving one disk from the source to the destination tower of choice. Other rules are not taken into account as there is only one disk. Going up, if we have two disks (n=2), we have added some complexity to the problem.
Figure 3: Solution where n=2
The number of steps needed for solving is now three, as we now have to consider how disks are stacked onto each other. When n=3, complexity goes further up. Now the manipulation of disks really is starting to get complicated.
Figure 4: Solution where n=3
Number of steps now rises to 7.
Observing those cases, we can draw some conclusions:
- the number of cases needed for solving the puzzle is 2^n-1 (which suggests the problem has the exponentially rising complexity),
- when number of disks is greater than 1, the problem corresponds to the moving of the n-th disk to the destination tower, while n-1 disks are firstly moved to the auxiliary tower in order to be decomposed into single disks which are further moved until they all end up sorted from the smaller to bigger onto a destination tower,
- the recursive nature of the problem is revealed in the same moving pattern of n-1 disks (regardless of the size of n), which is subdivided into smaller, recursive (sub)patterns of the same nature.
Aforementioned conclusions can help us devise the algorithm in pseudo-code:
- if the n=1, it’s a base case,
- move n-1 disks from source to the auxiliary tower first,
- move nth disk from source to the destination tower,
- move n-1 disks from auxiliary to destination tower.
Whenever the disk moves, algorithm should notify the user, ultimately giving the print-out of the steps taken in order to solve the puzzle. The total number of steps should be at minimum 2^n-1, which can be utilized in order to control the validity of the algorithm. The recursive calls should dismount the calls to itself all up to the base case, which is where n=1. Implementation of algorithm in Python We start by defining the function and its parameters. The parameters we will pass to the function will be, as previously noted number of disks, and the three towers. Using if check we can check for the base case. So, we literally translate the presented pseude-code to Python code:
1
2
3
def hanoi(n, source, dest, aux):
if n==1:
print(source, " to ", dest)
Now we need to define the else cases. It will be the part where the recursive calls are found.
1
2
3
4
else:
Hanoi(n-1, source, aux, dest)
print(source, " to ", dest)
Hanoi(n-1, aux, dest, source)
Combining it all together:
1
2
3
4
5
6
7
def hanoi(n, source, dest, aux):
if n==1:
print(source, " to ", dest)
else:
hanoi(n-1, source, aux, dest)
print(source, " to ", dest)
hanoi(n-1, aux, dest, source)
Evaluation of the code
We test the written function by calling it for cases where n=1 to n=4.
1
hanoi(1,1,3,2)
Output:
1
1 to 3
This is the base case, we get the expected result, as the disk is transferred from the source to destination tower in one step.
1
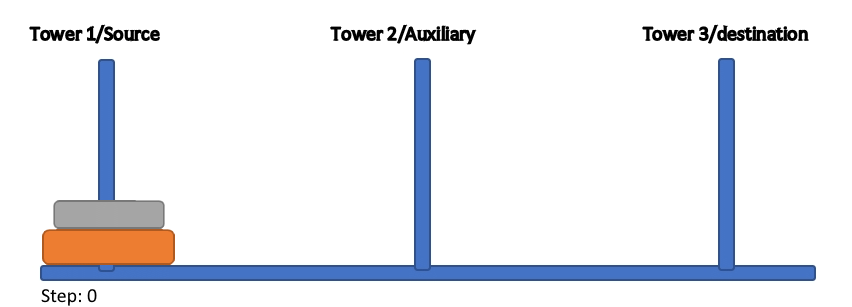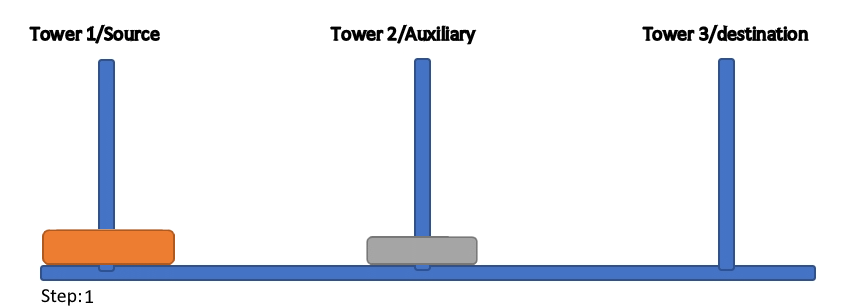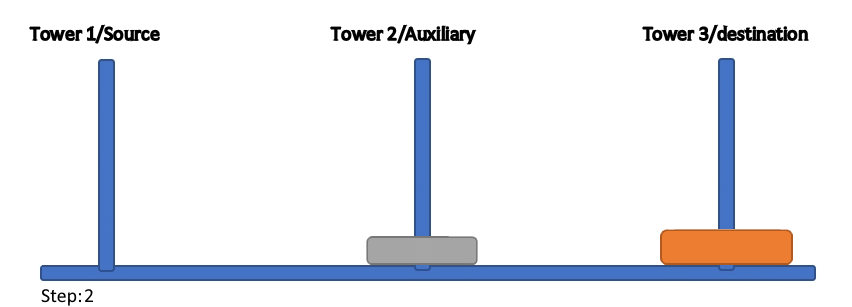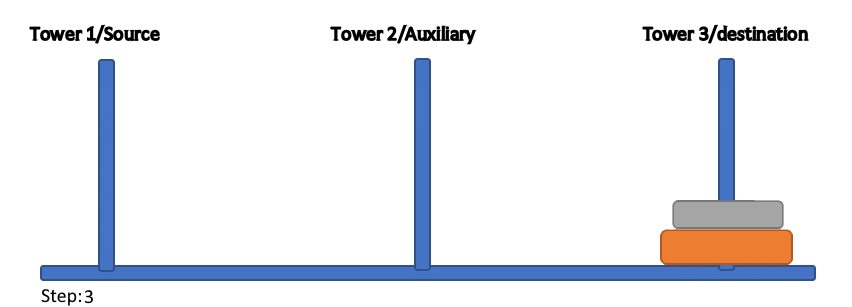
hanoi(2,1,3,2)
Output:
1
2
3
1 to 2
1 to 3
2 to 3
Here we see how the function is calling itself:
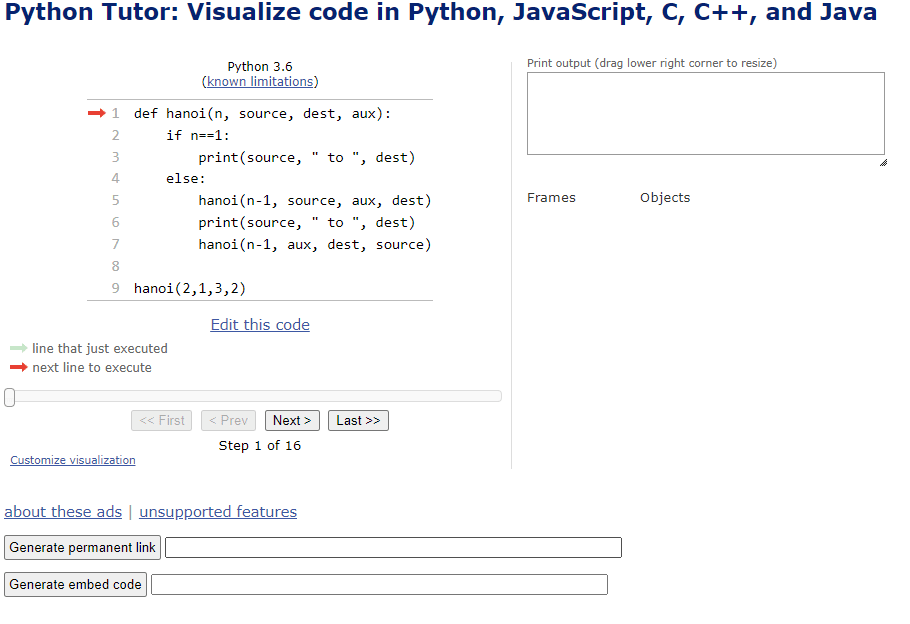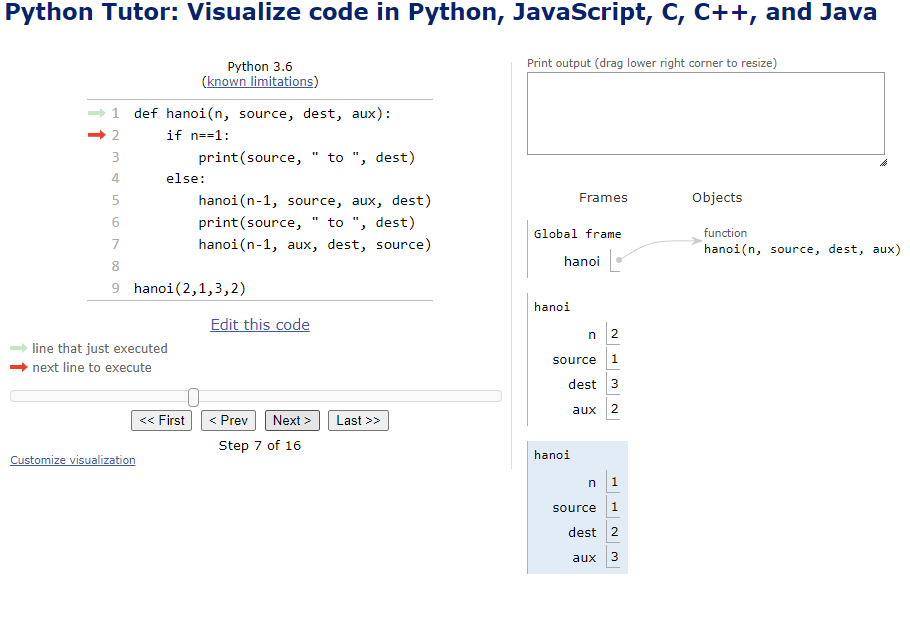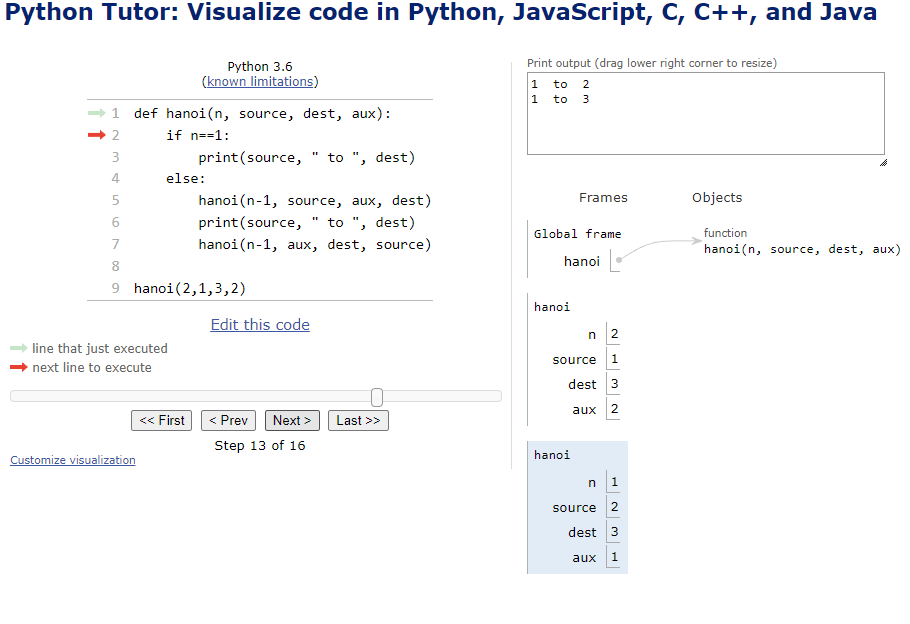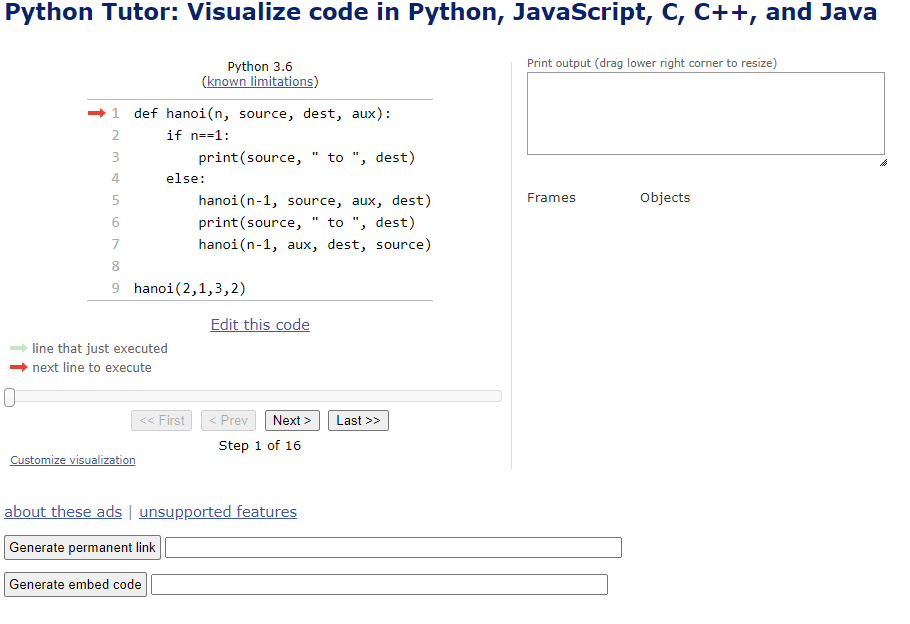Figure 5: Visualization of the code where n=2, using https://pythontutor.com/
The total number of steps is 3, which is within the established limit of 2^n-1.
1
hanoi(3,1,3,2)
Output:
1
2
3
4
5
6
7
1 to 3
1 to 2
3 to 2
1 to 3
2 to 1
2 to 3
1 to 3
Figure 6: Visualization of the code where n=3, using https://pythontutor.com/
Again, the total number of steps is within the parameter’s range.
1
hanoi(4,1,3,2)
Output:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1 to 2
1 to 3
2 to 3
1 to 2
3 to 1
3 to 2
1 to 2
1 to 3
2 to 3
2 to 1
3 to 1
2 to 3
1 to 2
1 to 3
2 to 3
The total number of steps is confirmed for this case as well.
Conclusion
Towers of Hanoi is the famous puzzle which is introduced in the West at the end of the 19th century, yet it was known for centuries before in the Far East. It is one of the prime examples of recursion. If one truly dives deep enough, the beauty of the code calling itself is astonishing: in only a couple of code’s lines we have defined a universal solution to the problem regardless of the size of n. The iterative solution is more complex and not so intuitive like the recursion one.